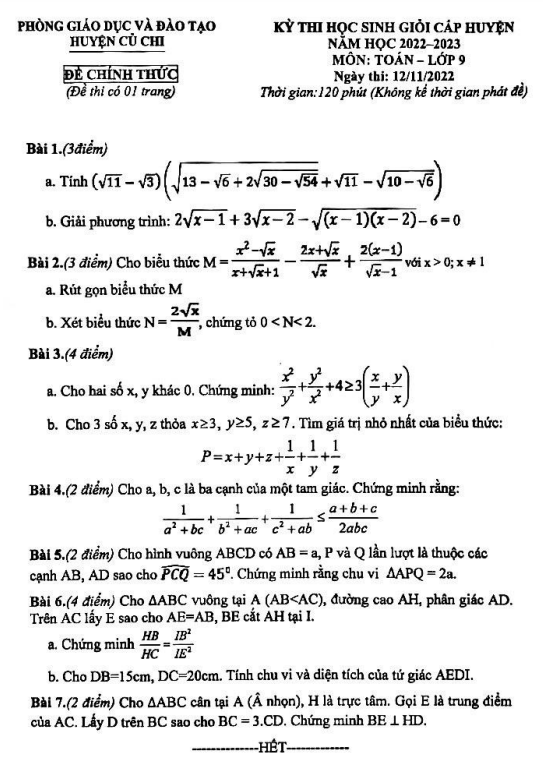Đề học sinh giỏi Toán 9 năm 2022 – 2023 phòng GD&ĐT Hoàng Mai – Nghệ An

Trích dẫn Đề học sinh giỏi Toán 9 năm 2022 – 2023 phòng GD&ĐT Hoàng Mai – Nghệ An:
+ Cho tam giác ABC có 3 góc nhọn, vẽ đường cao AD và BE. Gọi H là trực tâm của tam giác ABC. a) Chứng minh: AD.DH = DB.DC và tanB.tanC = AD/HD. b) Gọi a, b, c lần lượt là độ dài các cạnh BC, CA, AB của tam giác ABC. Chứng minh rằng.
+ Cho tam giác ABC vuông cân tại A và M là điểm di động trên đường thẳng BC (M khác B, C). Hình chiếu của M trên các đường thẳng AB và AC tương ứng là H và K. Gọi I là giao điểm các đường thẳng CH và BK. Chứng minh rằng các đường thẳng MI luôn đi qua một điểm cố định.
+ Cho tam giác ABC có độ dài các cạnh là a, b, c sao cho thỏa mãn hệ thức 20bc + 11ac + 1982ab = 2022. Tìm giá trị nhỏ nhất của biểu thức M (trong đó p là nửa chu vi tam giác ABC).